ABstrak

Read More

Weeding Esty dan Umar

Read More

“KETAKHINGGAN (INFINITY)”/PORTOFOLIO 1

MATEMATIKA MODEL

(TUGAS PORTOFOLIO)

“KETAKHINGGAN (INFINITY)”

Oleh:

IMALUDIN AGUS

NIM.15709251038

Tugas ini ditulis Sebagai Tugas Mingguan Mata Kuliah Matematika Model dengan Dosen Pengampu Bapak. Prof. Dr. Marsigit, MA.

PENDIDIKAN MATEMATIKA

PROGRAM PASCASARJANA

UNIVERSITAS NEGERI YOGYAKARTA

YOGYAKARTA

2016

Ketakhinggan (Infinity)

Matematika merupakan ilmu yang syarat akan symbol. Matematika memiliki banyak symbol yang didefinisikan secara jelas untuk setiap pemaknaanya. Oleh karena banyaknya symbol dengan makna yang berbeda dalam matematika, maka inilah yang menjadi salah satu penyebab mengapa matematika sulit dipahami oleh setiap yang awam dalam matematika.

Salah satu simbol yang menarik untuk dibahas dalam matematika adalah tak hingga (Infinity) atau biasa dinotasikan dengan ∞. Tak hingga (Infinity) adalah sebuah konsep abstrak yang menggambarkan sesuatu yang tanpa batas dan relevan dalam sejumlah bidang, terutama matematika dan fisika. Selain itu, pendapat lain juga mengungkapkan bahwa tak hingga ialah tiap bilangan (kecuali 0) yang dibagi oleh 0 sehingga bernilai tak hingga.

Sejarah tak hingga (Infinity) dimulai pada masa awal yunani. Tak hingga (Infinity) diperkenalkan oleh salah satu filsuf yang bernama Anaximander. Dia mengungkapkan kata “apeiron” yang berarti tak terbatas. Akan tetapi, awal pembuktian tak hingga (Infinity) matematika dilakukan oleh Zeno dari Elea (C 490 SM- C 430 SM). Seorang filsuf yunani pra sokrates dari selatan italia dan anggota Eleatic sekolah yang didirikan oleh Paramenides.[1]

Aristoteles memanggilnya penemu dialektika. Dia terkenal karena paradoksnya yaitu paradox Achilles dan kura-kura. Paradox ini terkenal karena orang yunani gagal menjelaskan paradox ini. Zeno menganalogikan paradox ini dengan membayangkan lomba lari Achilles dan seekor kura-kura. Keduanya dianggap lari dengan kecepatan konstan dan kura-kura sudah tentu jauh lebih lambat. Untuk ittu, si kura-kura diberi keuntungan dengan start awal didepan, katakanlah 10 m (titik dimana kura-kura mulai). Tetapi si kura-kura ini juga pasti sudah melangkah maju jauh lebih lambat memang, katakanlah dia baru melangkah 1 meter. Beberapa saat kemudian Archilles berada dititik 11 m, tetapi sikura-kura sudah melangkah maju sebesar 0,1 m. Demikian seterusnya setiap kali Achilles berada pada titik dimana kura-kura sebelumnya berada si kura-kura sudah melangkah lebih maju. Artinya secepat apapun Achilles, tidak akan pernah mendahului kura-kura.

Kasus tersebut diatas, dapat terpecahkan setelah pada awal abad ke 17 juga para ahli matematika telah menangani deret tak hingga diantaranya adalah Rene Deskrates (1596-1650). Descartes telah memecahkan kebuntuan dari beberapa abad, yakni dapat menjelaskan paradox Zeno secara memuaskan dengan menggunakan limit jumlah deret tak hingga. Berdasarkan formula tersebut, maka diperoleh jarak yang diperlukan oleh Achilles untuk menyusul kura-kura yang membentuk deret geometri tak hingga: [2]

10 + 0.1 + 0.01 + ….

Dengan rasio perbandingan r = 0.1.

Pembangian bilangan tak hingga dalam matematika dilakukan pada tahun (abad 3 - 4 SM) oleh India Surya Prajnapti, dimana bilangan diklasifikasikan menjadi 3 bagian yakni:

1.      Dapat dihitung, terendah, menengah dan tinggi

Contoh:

Himpunan bilangan asli yang kurang dari 5 (1,2,3,4)

2.      Tak terhitung, hampir tak terhitung, benar-benar tak terhitung dan tak terhitung banyak

Contoh:

Himpuan semua bilangan asli (1,2,3,4…)

3.      Tak Terbatas, yang tidak terbatas, tak terhingga

Contoh:

Selain itu, untuk penggunaan notasi ∞ pertama kali dilakukan oleh John Wallis pada Abad 17. Wallis menuliskan suatu formula yaitu suatu bilangan yang dibagi oleh nol (0) selain nol itu sendiri memiliki hasil tak hingga atau dalam matematikanya adalah sebagai berikut :

.[3]

Pandangan lainnya, seperti yang diungkapkan oleh Santo Agustinus dan Immanuel Kant, dimana Agustinus mengemukakan bahwa tak hingga sesungguhnya lebih banyak bersifat keagamaan sedangkan kant mengatakan ketakhinggan menyangkut ruang, waktu, serba terus, diskrit, sebab-akibat, dan kebetulan.

Setelah membahas mengenai asal mula adanya istilah tak hingga (Infinityf), maka muncul sebuah pertanyaan dari mana munculnya notasi tak hingga (Infinityf) yakni “∞”? Notasi “∞” diperkirakan berasal dari varian pada Ouroboros klasik. Ouroboros merupakan siklus abadi hidup dan tak terbatas, konsep keabadian dan kembali abadi, dan merupakan siklus hidup, kematian, dan kelahiran kembali seperti phonenix. [4]

---

[1] http://www.slideshare.net/ratumugita/materi-50349096

[2] Ibid

[3] http://kopicopi.blogspot.co.id/2014/01/penemu-simbol-bilangan-tak-terhingga.html

[4] http://klinikunique.blogspot.co.id/2011/08/ouroboros-makna-dari-salah-satu-simbol.html

Read More

MAKALAH UJIAN AKHIR SEMESTER FILSFAT ILMU "MAKALAH TENTANG PEMAHAMAN AWAL TENTANG FILSAFAT"

FILSFAT ILMU

(MAKALAH HIPOTETYCAL ANALYSIS)

“PEMAHAMAN AWAL TENTANG FILSAFAT”

Oleh :

IMALUDIN AGUS

NIM.15709251038

Tugas ini ditulis untuk memenuhi sebagian persyaratan untuk tugas akhir mata kuliah Filsafat Ilmu dengan dosen pengampu Bapak. Prof. Dr. Marsigit, MA.

PENDIDIKAN MATEMATIKA

PROGRAM PASCASARJANA

UNIVERSITAS NEGERI YOGYAKARTA

YOGYAKARTA

2016

PENGETAHUAN AWAL TENTANG FILSAFAT

PENDAHULUAN

Filsafat merupakan olah pikir. Filsafat mendorong setiap individu yang ingin mengenalnya untuk mengetahui apa yang diketahui dan apa yang belum diketahui. Setiap yang mempelajari filsafat diharapkan untuk mampu berendah hati sebab semakin kita mempelajari filsafat semakin kita menyadari bahwa kita semakin tidak mengetahui apa-apa, dan apa yang telah kita ketahui tidak lebih dari setitik tinta yang dicelupkan dalam lautan luas. Hal ini sejalan dengan apa yang diungkapkan oleh Sokrates bahwa “satu hal yang saya tahu yaitu saya tidak mengetahui apa-apa”.

Kerendahan hati sokrates menunjukan bahwa betapa menyadarkan kita berfilsafat bagaikan memasuki rongga kecil yang memiliki ruangan yang luas dan tak terhingga luasnya yang meliputi seluruh jagad raya dan isinya. Dengan ruang yang cukup luas ini mengantarkan pemiliki kemampuan menalaran dan komunikasi yakni manusia untuk mencoba mengenal semua gejala yang terjadi sedetail mungkin walaupun dengan keterbatasan daya dan kemampuan yang dimiliki. Hal ini disebabkan manusia adalah ciptaan Allah SWT yang paling sempurna didalam ketidak sempurnaan, sebab jika manusia sempurna maka artinya tidak hidup.

Pada dasarnya, filsafat memiliki dua objek yang utama yaitu yang ada dan yang mungkin ada, baik yang didalam pikiran maupun diluar pikiran. Akan tetapi, yang menjadi pertanyaan adalah apa yang ada dalam pikiran dan yang mungkin ada dalam pikiran? Serta apa yang ada dan yang mungkin ada diluar pikiran? Kedua pertanyaan ini merupakan pertanyaan mendasar bagi setiap orang awam yang baru mengenal filsafat sebab bagaimana bisa memahami filsafat secara ekstensif dan intensif jika objek kajiannya saja masih buram.

Selain objek filsafat, pemahaman terhadap aspek-aspek filsafat juga menjadi hal penting, dimana filsafat terbagi atas tiga aspek yaitu ontologi, epistomologi dan aksiologi. Ontology membahas tentang hakikat yang ada, epistomologi lebih diidentikkan dengan pengetahuan serta aksiologi terbagi atas dua bagian utama yakni etika (baik dan buruk) serta estetika (indah dan jelek).  Akan tetapi, setiap objek serta aspek dalam filsafat harus selalu ada dalam koridor atau kriteria kebenaran menurut filsafat, yang mengharuskan setiap yang mencoba mengenalnya untuk patuh dan taat pada ruang dan waktu, sebab kebenaran menurut filsafat jika sesuai dengan ruang dan waktu serta kesalahan itu karena tidak sesuai dengan ruang dan waktu. Oleh karena itu, untuk pemahaman lebih jauh mengenai dasar-dasar filsafat maka dipandang perlu adanya penjelasan mengenai apa itu filsafat? Bagaimana objek filsafat? Apa saja aspek-aspek dari filsafat? Serta bagaimana pandangan filsafat mengenai yang benar dan yang salah?

PEMBAHASAN

Filsafat adalah olah pikir. Olah pikir diartikan sebagai kemampuan menggunakan pikiran dan penalaran untuk mempertanyakan dan meragukan setiap apa yang ada dan yang mungkin di alam semesta serta berusaha untuk menjawab setiap perntanyaan dan membuktikan setiap yang diragukan. Hal ini sejalan dengan yang diungkapkan oleh Rene Deskrates bahwa “Saya ada karena saya berpikir”. Oleh karena itu, esensi utama dari filsafat adalah berpikir dan bagaimana menggunakan pikiran untuk mengungkap semua objek dari filsafat.

Secara subtansial, yang dipikirkan dalam filsafat yaitu tentang yang ada dan yang mungkin ada. Menurut Aristotels dikatakan ada dalam pikirian jika objek yang dimaksud dapat dilihat, diraba, dirasakan atau secara umum dapat terdeteksi oleh pancaindra manusia. Paham seperti ini disebut paham Realisme. Sedangkan pandangan lain tentang yang ada yaitu menurut Plato, sesuatu dikatakan ada jika ada dalam pikiran yang berupa logika, sebagai salah satu contoh real mengenai hal ini adalah matematika murni, yang kebenarannya tergantung pada koherentismenya. Paham yang seperti diungkapkan oleh plato disebut platonisme atau biasa disebut idealisme.

Selanjutnya, filsafat dianalogikan sebagai penguasa utama dari segala lini dalam alam kesemestaan, yang membuka ruang untuk lini-lini lain berada didalamnya serta menjadi bagian dari kajiannya. Setiap yang mempelajari filsafat mengharuskan dirinya mampu membuka pikiran dan memperlebar pandanganya, bahwa dunia memiliki dimensi serta struktur yang luas atau menurut bahasa awamnya yakni “ada langit diatas langit”.

Selain itu, setiap manusia memiliki dimensi berpikir yang berbeda antara individu yang satu dengan individu yang lain tergantung bagaimana usaha manusia tersebut mengesplor dan meningkatkan dimensi berpikirnya. Salah satu contoh untuk meningkatkan dimensi berpikir manusia adalah melalui proses belajar secara kontinu baik disekolah formal maupun informal.

Filsafat menggunakan bahasa analog serta metode hidup sebagai alat untuk memahami dan mengungkapkan semua yang ada dan yang mungkin ada. Bahasa analog merupakan bahasa yang lebih halus dari bahasa kiasan, dimana setiap subtansi pikiran yang ingin diungkapkan tidak langsung dipahami secara gamblang oleh para pembacanya, akan tetapi harus memerlukan proses analisis yang logis serta melalui sintesis yang koheren. Sedangkan metode hidup diartikan sebagai   metode yang digunakan dalam mempelajari filsafat, dengan individu sebagai objek utama dan proses belajarnya disesuaikan dengan pengalaman dan kemampuan individu tersebut. Jika dikaitkan dalam proses pembelajaran matematika, maka metode hidup merupakan proses pemberian jalan kepada peserta didik untuk belajar sesuai dengan taraf berpikirnya serta guru harus memandang peserta didik bukan sebagai empty vessel, yang bisa diisi dengan apapun oleh gurunya. Akan tetapi, paradigma ini harus berubah menjadi peserta didik sebagai pribadi yang memiliki kemampuan berpikir, menalaran, mensintesis dan lain sebagainya yang dapat tereksplor dengan baik.

Secara fundamental, Filsafat merupakan induk dari segala pengetahuan yang memiliki batasan dan objek kajian masing-masing. Satu hal terpenting dalam belajar filsafat adalah mengetahui sampai mana batasan-batasannya, sehingga dalam proses memahaminya tidak menyimpang dari nilai-nilai ideal yang diharapkan serta tidak terjerumus dalam paradigma yang salah mengenai filsafat dan proses pemahaman jagad raya. Oleh karena itu, diperlukan fondasi agama yang kokoh sebagai tembok pembatas, sebab tujuan hidup bukan hanya dunia tetapi yang tak kalah lebih penting adalah akhirat. Seperti salah Ungkapan berikut “Berusahalah seakan-akan engkau hidup seribu tahun lagi dan beribadahlah seakan-akan engkau akan mati esok”.

Kaitannya dengan objek filsafat, maka pada dasarnya filsafat memiliki dua objek utama yaitu yang ada dan yang mungkin ada. Yang ada diartikan sebagai sesatu yang dapat dilihat, dirasakan oleh pancaindra manusia. Selain itu, dikatakan ada ketika ada dalam pikiran. Sedangkan yang mungkin ada diartikan sebagai sesuatu yang belum bisa dijangkau oleh pikiran manusia baik itu kejadian dimasa lampau maupun kejadian dimasa mendatang atau dalam bahasa filsafatnya disebut trasendental. Dari dua objek filsafat ini maka muncul dua pertanyaan mendasar mengenai esensi yang ada dan yang mungkin ada. Dua pertayaan tersebut yaitu jika ada diluar pikiran, bagaimana mengetahuinya? Serta jika ada dalam pikiran bagaimana mengungkapkannya?

Ketika berbicara ada dan yang mungkin ada, maka setiap individu memiliki perspektif yang berbeda, sebab bisa jadi ada bagi saya belum tentu ada bagi yang lain serta ada bagi yang lain belum tentu ada bagi saya. Sebagai ilustrasi sederhana yaitu ketika saya menyebutkan tanggal lahir adik saya maka tentu ada bagi saya tetapi mungkin ada bagi yang lain yang belum pernah mengetahui kapan adik saya lahir, begitupula sebaliknya.

Selain itu, setiap manusia hanya mampu berusaha menggapai setiap yang ada dan mungkin ada serta tidak mampu menyebutkan semua yang ada dan mungkin ada tersebut, baik yang ada dalam pikir maupun yang diluar pikiran, sebab manusia merupakan makhluk sempurna dalam ketidak sempurnaan. Oleh karena itu, dalam memahami setiap yang ada dan mungkin ada tergantung pada sejauh mana individu memiliki pengalaman dan intuisi yang diperolehnya dalam proses berkehidupan.

Selanjutnya, filsafat terbagi atas tiga aspek yaitu pertama, ontologi. Ontologi merupakan hakekat yang ada. Ada menurut filsafat jika terdapat didalam pikiran atau diluar pikiran. Ada diluar pikiran ketika tidak bisa dikenali dengan panca indra, akan tetapi dapat dianalisis oleh pikiran. Kedua aspek epistomologi. Epistomologi diartikan dengan pengetahuan, maka filsafat ilmu merupakan bagian dari aspek epistomologi. Ketika berbicara pengetahuan, maka ada sebuah pertanyaan besar dari mana sesungguhnya pengetahuan itu berasal? Menurut Immanuel kant pengetahuan merupakan hasil dari pengalaman manusia yang terus-menerus dan kebenarannya dibenarkan oleh logika atau dalam istilah filsafat disebut Intuisi. Selain itu, menurut Aristoteles pengetahuan hanya berdasarkan pengalaman manusia atau biasa disebu emperik. Oleh karena itu, pengetahuan berawal dari rasa ingin tahu dan meragukan setiap yang ada dan yang mungkin ada, sehingga dengan pengalaman, logika dan analisis yang dimiliki manusia, berusaha untuk mendukung atau membantah setiap apa yang dipertanyakan atau yang diragukan.

Aspek Ketiga yaitu aksiologi. Pada filsafat aksiologi diartikan sebagai kaidah, seni atau panduan mengenai baik dan buruk maupun indah dan jelek. Kedua bagian ini terkalasifikasi menjadi    dua bagian yang holistic yaitu etika dan estetika. Ketika berbicara etika maka kajian utamanya adalah mengatur bagaimana seharusnya tindakan yang harus dimiliki oleh setiap orang yang hendak mempelajarinya. Didalam etika menekankan pada apakah sesuatu itu baik atau buruk. Akan tetapi, untuk membuktikan mana yang baik dan mana yang buruk dalam filsafat merupakan hal yang relative, sebab filsafat sangat menghargai perbedaan ruang dan waktu serta meyakini bahwa setiap ruang dan waktu memiliki aturan dan tatacara yang berbeda, sehingga penentuan kriterian penilian benar atau salahnya pun akan berbeda. Sebagai contoh sederhana yaitu ketika mengatakan yang tidak sebenarnya kepada para penjahat mengenai sesuatu yang menjadi incarannya maka ini bernilai baik untuk ruang dan waktu tersebut, tetapi akan bernilai buruk ketika perkataan dan perlakukam tidak jujur dipergunakan dalam pemerintahan, maka tentu imbasnya adalah penyalahgunaan wewenang serta perampasan terhadap hak-hak orang dibawahnya, Seperti bawahan maupu masyarakatnya.  

Sejalan dengan pernyataan diatas maka estetika yang merupakan bagian dari aksiologi dan memiliki peranan dalam hal penentuan keindahan atau tidak indah, maka tentu tidak akan terlepas pula pada keterkaitanya dengan ruang dan waktu. Ruang dan waktu merupakan patokan utama dalam penentuan suatu kriteria dan bagimana tolak ukur yang dapat dipergunakan sebagai alat validasi. Seperti halnya pada etika, maka estitika antara tempat yang satu dengan tempat yang lain akan berbeda. Perbedaan ini terletak pada budaya serta aturan yang diterapkan didaerah atau wilayah tersebut. Sebagai ilustrasi sederhana, budaya barat yang sangat bertentang dengan budaya timur, dimana menurut budaya barat fashion, gaya bergaul, serta gaya hidup yang hedonis dan bebas merupakan hal yang indah, tetapi menurut budaya timur memiliki nilai yang negative dan bahkan merupakan aib besar yang harus dihilangkan.

Oleh karena itu, dengan berfilsafat mengajarkan kepada setiap individu menyadari sejauh mana batasan yang dimilikinya serta tidak menjadikan dirinya sebagai pribadi yang sombong, sebab manusia adalah makhluk yang penuh salah dan dosa serta keterbatasan. Selain itu, kesadaran terhadap ruang dan waktu merupakan hal penting untuk selalu peka terhadap kedua aspek ini, agar dalam segala tindakan yang hendak dilakukan sesuai dengan kriterian kebenaran yang tepat berdasarkan ruang dan waktu yang tepat pula. Selanjutnya, saya mengutip apa yang diungkapkan oleh Albert Enstein bahwa “agama tanpa ilmu adalah sesat dan ilmu tanpa agama adalah buta”. Ungkapan ini merupakan penanda bagimana pentingnya agama dalam proses memahami setiap yang ada dan yang mungkin ada, agar setiap diri selalu berada pada right trace (Jalan yang benar) yang telah Allah berikan dan diamanahkan kepada semua umat manusia.

PENUTUP

KESIMPULAN

Berdasarkan pendahuluan dan pembahasan diatas, maka yang dapat disimpulkan dalam makalah hipotetycal analysis yang berjudul pemahaman awal tentang filsafat yaitu sebagai berikut:

a.       Filsafat ilmu merupakan oleh pikir, dengan bahasa analog sebagai alat bantu komunikasinya serta metode hidup sebagai metodologis yang tepat untuk mempelajarinya. Bahasa analog adalah bahasa yang lebih halus dari bahasa kiasan yang mengharuskan adanya proses berpikir dalam memahami setia yang ada dan mungkin ada. Sedangkan metode hidup yaitu metode yang memandang individu sebagai pribadi yang memiliki karakteristik yang berbeda dan unik, sehingga dalam proses belajarnya pun harus berdasarkan pada kemampuan dan pemahaman mereka, sebab filsafat adalah diri kita sendiri.

b.      Filsafat memiliki dua objek utama yaitu yang ada dan yang mungkin ada. Yang ada diartikan sesuatu yang dapat dijangkau oleh panca indra dan pikiran serta yang mungkin ada diartikan sesuatu yang tidak bisa dijangkau oleh panca indra dan pikiran, baik kejadian dimasa lalu maupun kejadian dimasa mendatang. Satu hal yang harus diperhatikan adalah yang ada dan yang mungkin ada antara individu yang satu dengan individu yang lain akan berbeda, sebab ada untuk saya belum tentu ada untuk yang lain dan begitu pula sebaliknya.

c.       Filsafat memiliki 3 aspek yaitu ontologi, epistomologi, dan aksiologi. Ontology diartikan sebagai hakikat yang ada, epistomologi diartikan sebagai pengetahuan dan filsafat ilmu merupakan bagian dari aspek ini. Sedangkan aksiologi berkaitan erat dengan etika dan estetika. Etika memiliki kajian dalam hal penentuan tindakan baik atau buruk sedangkan estetikan memiliki fungsi sebagai penentu kriteria indah atau jelek.

d.      Filsafat memandang setiap yang salah dan yang benar sebagai sesuatu hal yang relatif, sebab filsafat sangat patuh pada ruang dan waktu. Ruang dan waktu merupakan tolak ukur yang menjadi dasar penyusunan kriteria kebenaran, agar alat ukur yang digunakan untuk mengungkapkan kebenaran maupun kesalahan memang benar-benar valid.

Read More

FILSAFAT MATEMATIKA

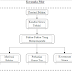
FILSAFAT MATEMATIKA

Penjelasan :

1.       Orang Awan, berarti ukuran ubin sebab dengan 30 cm x 30 cm = 900 cm²  secara kontekstual dilapangan lebih sering dijumpai sebagai ukuran ubin

2.       Idiologi, Formal sebab 30 cm x 30 cm = 900 cm²  formal dari luas

3.       Budaya, Karya sebab 30 cm x 30 cm = 900 cm²  karya atau cara untuk mencari luas

4.       Ada, 30, 30, =, 900 x,cm, cm² , sebab setiap pengada pasti dibentuk dari beberapa yang ada

5.       Mengada, 30 cm x 30 cm, sebab untuk menjadi pengada harus melalui proses mengadakan terlebih dahulu

6.       Sekolah, Geometri sebab pada pembelajaran disekolah ketika berbicara cm² maka ini berarti pokok materinya adalah geometri

7.       Guru, Bangun Datar sebab 30 cm x 30 cm = 900 cm² adalah proses memcari luas bangun datar

8.       Siswa, Luas Persegi sebab persegi memiliki sisi yang sama panjang

9.       Metode, Kontekstual, Realistik atau PBL, sebab 30 cm x 30 cm = 900 cm²  merupakan contoh konkret atau masalah konkrit yang berkaitan dengan luas persegi

10.   Kurikulum, kurikulum 2013 sebab kurikulum 2013 menekankan pada pemecahan masalah dan kontekstual yang bersumber dari lingkungan seperti contoh ukuran ubin tersebut

11.   Formal terbagi dua yaitu luas Persegi dan integral, kedua rumus tersebut merupakan cara untuk mencari luas daerah

12.   Epistomologi, wadah  atau isi dari 30 cm x 30 cm = 900 cm²   yang merupakan bagian dari pengetahuan untuk mencari luas daerah

13.   Ontologis, benar atau salah dari 30 cm x 30 cm = 900 cm²  

14.   Aksiologi, subjektif sebab untuk menilai indah atau buruknya tergantung pada subjek yang menilainnya.

15.   Sosiologi, daerah atau wilayah sebab ketika berbicara luas maka ini berkaitan dengan luas wilayah, dll

16.   Psikologi, memperluas sebab psikologi berkaitan dengan tindakan

17.   Spritual, keluasaan beribadah sebab kata luas dalam spiritual secara mutlak berhubungan dengan keluasan beribadah kepada Allah agar kita juga mendapatkan keluasan, kelapangan dan ridhonya. 

Read More

An Onto-Semiotic Analysis of Combinatorial Problems and The Solving Processes by University Students

Kelompok 1

Review Jurnal Penenlitian Deskripsi Eksploratif

Imaludin Agus           15709251038

Venti Indiani              15709251057

Tri Kurniah L           15709251065

Judul           : An Onto-Semiotic Analysis of Combinatorial Problems and The Solving Processes by University Students

Penulis            : Juan D. Godino, Carmen Batanero, dan Rafael Roa

Intisari

Menurut Ernest (1988) matematika adalah suatu kegiatan atau aktivitas. Dalam aktivitas tersebut timbul gejala atau respon baik berupa visual maupun verbal. Pada penelitian ini hal tersebut dianalisis dengan metode ontologis semiotik untuk melihat kemampuan berpikir matematis pada mahasiswa. Semiotik berasal dari kata sign yang berarti tanda. Secara umum metode semiotik dapat diartikan sebagai suatu metode dengan melihat tanda yang muncul baik secara visual maupun verbal.

Entitas utama dari ontologis semiotik terdiri dari enam entitas, yaitu: bahasa, situasi/masalah, tindakan, konsep, properti, dan argumen.

Bahasa

Penyajian yang digunakan untuk mewakili masalah kombinatorial ini yaitu notasi simbolik dan susunan tabel (tabulasi arrangement),  contoh notasi simbolik : kombinasi antara 3 huruf identik yang dimasukan secara berturut-turut kedalam 4 amplop, notasi simboliknya yaitu : C(n,m), C(4,3). Kemudian contoh susunan tabel nya seperti combinasi segitiga pascal, diagram venn, dan pohon.

Situasi/Masalah

Masalah kombinatori merupakan masalah pada matematika yang menyebabkan  munculnya aktivitas kombinatorial.

Soal 1 :

Kombinasi tiga angka yang diambil berturut-turut dalam kotak yang berisi 4 kelereng.

Soal 2:

Kita memiliki 3 huruf yang identik  yang akan dimasukan kedalam 4 amplop yang berbeda warna. Solusi untuk masalah ini adalah C4,3, tetapi ada banyak kemungkinan yang berbeda dalam model ini, tergantung pada fitur berikut:

Soal 3 :

Seorang anak laki-laki memiliki empat mobil yang berbeda warna (hitam, oranye, putih dan hijau) dan dia memutuskan untuk memberikan mobil tersebut kepada teman-temannya Fernando, Luis dan Teresa. Berapa banyak cara yang berbeda ia dapat mendistribusikan mobil tersebut?

Soal 4: seorang anak memeliki 12 kartu permainan : 9 kartu diberi nomor dengan angka 1, 2, 3, 4, 5, 6, 7, 8 dan 9. Kemudian tiga kartu yang tersisa diberi nama: jack, ratu dan raja. Berapa banyak cara yang berbeda dalam mengatur empat kartu berturut-turut, dengan kondisi bahwa tiga kartu yang diberi nama selalu dipilih?

Tindakan

Ketika dihadapkan dengan masalah matematika diperlukan tindakan yang beragam dalam proses penyelesaiannya. Sehingga diharapkan siswa dapat melakukan tindakan berikut untuk memecahkan masalah :

a. Menerjemahkan pernyataan masalah

b. Mengidentifikasi kondisi sampel

c. Menyadari kondisi dimana dimungkinkan untuk menerapkan konsep

d. Mengingat dan beroperasi dengan rumus

e. Melaksanakan operasi aritmatika

Konsep

Selain memahami  cara memecahkan masalah dengan notasi yang mereka gunakan, diharapkan siswa juga dapat memahami konsep-konsep mengenai kombinasi, kelompok, parameter, seleksi, permutasi dan lain sebagainya.

Properti

Konsep ditentukan oleh atribut (sifat) yang mewakili kondisi, dan karakteristik dalam suatu situasi serta hubungan antar objek contohnya suatu kombinasi diperoleh dari pembagian antara susunan yang mungkin dan permutasi.

Argumen

Semua tindakan yang dilakukan melalui argumen atau penalaran, digunakan untuk memeriksa solusi masalah dan menjelaskan solusi ini kepada orang lain.

Aspek pengetahuan matematika dapat dilihat berdasarkan dua aspek yang berpasangan: personal-institusional, ostensive-non ostensive, example-type, elemental-systemic, expression-content.

personal-institusional

Dari segi institusional, sebelum melakukan evaluasi terhadap hasil tes pengetahuan siswa terlebih dahulu mengalisis buku teks dan kurikulum. Dari hasil analisis tersebut diperoleh bahwa interpretasi yang diberikan kurang jelas sehingga menyulitkan siswa untuk menemukan solusi dari permasalahan tersebut. Sedangkan dari segi individu, dimana pedro sebagai subjeknya ditemukan bahwa pedro mengalami kesulitan dalam menerapkan defenisi dan rumus kombinasi dalam pemecahan masalah, hal ini didasarkan pada hasil wawancara peneliti terhadap pedro. Selain itu, persoalan lain diperoleh bahwa pedro mengalami kesulitan dalam memahami dan mengidentifikasi masalah, sehingga mengalami kesalahan dalam penentuan solusi berdasarkan kerangkan yang dibuat oleh institusional

ostensive-non ostensive

Ostensive merupakan suatu cara menggambarkan suau konsep, sifat, masalah, pendapat(argument) serta tindakan yang diberikan melalui bahasa. Selain itu, juga merupakan salah satu cara untuk mengepresikan benda non ostetensif. Sebagai contoh: pada kasus pedro, dimana pedro mengasumsikan bahwa mobil yang diberikan kepada ketiga anak tersebut memiliki warna yang berbeda sehingga memungkinkan keempat mobil tersebut diperoleh oleh satu induvidu (Fernando). Kesimpulannya adalah harus memberikan penjelasan yang jelas terhadap objek yang digambarkan.

example-type

Gagasan yang dituliskan pada aspek ini tentang kesulitan membedakan antara jenis dan contoh dalam proses pemecahan masalah matematika. Salah satu contoh kasusnya adalah adolf yang mampu menyelesaikan masalah kombinasi tertentu dengan menggunakan pendekatan konkrit (tanpa rumus yang telah ditentukan) serta dapat digeneralisasikan dalam situasi lain.

elemental-systemic

Pada proses pembelajaran matematika (kombinatori) harus memperhatikan sistematik materi atau hubungan antara sub materi. Sebagai contoh hubungan antara kombinasi dengan nomor kombinasi, segitiga pascal serta hubungan kombinasi dengan binomial.

expression-content

Kegiatan matematika pada dasarnya relasional, dimana ada korespondensi antara antesenden (ekspresi, signifikasi) dan kosekuen (isi dan makna) yang didasarkan pada kriteria tertentu.

Berdasarkan hasil analisis pemecahan masalah yang dilakukan oleh mahasiswa pada materi kombinatorial dapat didapatkan beberapa hal. Hasil analisis pada penyelesaian permasalahan yang dilakukan oleh Adolf (subjek 1) diidentifikasi bahwa Adolf mampu mengidentifikasi semua data pada soal dengan benar. Dalam proses menyelesaikan masalah Adolf mengerjakan soal secara bertahap melalui step-step. Solusi yang dihasilkan oleh Adolf mempunyai tingkat kompleksitas yang relatif tinggi. Selain itu Adolf juga mempunyai argumen untuk memvalidasi solusi yang diperolehnya. Sementara itu Hasil analisis pada penyelesaian permasalahan yang dilakukan oleh Luisa (subjek 2) diidentifikasi bahwa dia pernah mendapat materi kombinasi sebelumnya dan dia masih ingat beberapa rumus namun kesulitan dalam memecahkan masalah. Luisa dapat menafsirkan data dengan baik dan menuliskan notasi symbol yang sesuai. Misalkan: notasi B : untuk Mobil Hitam. Luisa juga dapat menafsirkan beberapa pernyataan dan dia memahami objek yang didistribusi memiliki sifat yang berbeda dan dikelompokkan sesuai dengan sifatnya. Selain itu Luisa dapat menyelesaikan masalah dengan menggunakan rumus yang dia ketahui, tetapi terkadang ia kesulitan dalam menafsirkan masalah. Sementara itu hasil analisis pada penyelesaian permasalahan yang dilakukan oleh Juan (subjek 3) diidentifikasi bahwa ia sulit mengingat defenisi tentang materi kombinatorik serta mengalami kesulitan dalam penggunaan konsep atau operasi kombinatorik. Juan menafsirkan permasalahan (simbolisasi permasalahan) dengan benar. Dia juga mampu mengidentifikasi dengan benar fakta-fakta dalam masalah tersebut serta menerapkan dan mengidentifikasi operasi (konsep) secara langsung dalam proses pemecahan masalah berkaitan dengan materi kombinasi. Selain itu Juan menggunakan defenisi yang dibuatnya untuk langsung mengidentifikasi operasi (konsep) dalam proses pemecahan masalah.

Kelebihan

Kelebihan yang dapat dikemukakan dalam penelitian ini adalah sebagai berikut:

1.    Dapat menjelaskan lebih detail mengenai subjek penelitian

2.    Data dapat menyebabkan saran hipotesis untuk studi masa depan

3.    Hasil Penelitian dapat menjadi referensi, pedoman atau acuan bagi pendidik dalam proses evaluasi pembelajaran khususnya materi kombinatorik

Kelemahan

Kelemahan yang dapat dikemukakan dalam penelitian ini adalah sebagai berikut:

1.    Desain penelitian fleksibel sehingga hasil penelitian tidak bisa diprediksi.

2.    Hasil penelitian hanya berlaku untuk subjek yang diteliti saja.

3.    Tidak semua hasil pekerjaan siswa dianalisis secara detail.

Manfaat

Manfaat umum

Penelitian ini dapat digunakan sebagai kerangka teori dalam penyusunan tesis maupun jurnal untuk dipublikasikan.

Manfaat khusus

Bagi guru

Memberikan penjelasan lebih lanjut pada kesulitan dan keterbatasan dalam pembelajaran matematika berdasarkan sifat dan kompleksitas objek matematika.

Bagi peneliti

Sebagai bahan atau acuan yang relevan bagi penelitian selanjutnya.

Read More